New API endpoint for MathpixOCR (beta)

New API endpoint for text

We are happy to announce that our new API endpoint v3/text is now in public beta. We highly recommend that search and typesetting apps switch to using this new endpoint. After a few months of testing and bugfixes, we plan to remove the beta flag. The API specs for v3/text are available at https://docs.mathpix.com/#process-image-v3-text-beta.

The goal of v3/text was to provide a simpler and more robust way of extracting all math and all text in an image. It uses a different algorithm that is much better at reading a large amount of text. Traditionally, MathpixOCR has always struggled at reading more than a single paragraph at a time. Now, we can read up to a full page of mixed text and math (although we don’t support double columns yet). Text is represented as simple text (instead of using \text), inline Latex is enclosed in inline delimiters (by default \( ... \)), and block mode Latex is enclosed inside block mode delimiters (by default \[ ... \]). We chose these defaults because they are standard in modern Latex and Markdown editors.

New features

v3/text strips newlines, except in cases where they are semantically important, whereas v3/latex returns all newlines that appear visually
v3/text currently only returns text and latex_styled output options; text is always set in the response JSON if there’s readable text in the image. On the other hand, latex_styled is not returned when in the input is a text heavy image; in some cases there is ambiguity about whether latex_styled (math mode) and text (text mode) make more sense for a given image; in such cases we return both options
multiple choice questions are represented one line at a time in v3/text
text and latex_styled contain newlines in math mode when they make sense in order to make the resulting Latex code more readable

Limitations

not available in batch API yet
still in beta, bugfixes coming soon

Examples

Just text

returns:

By inserting a dielectric material between the plates of a parallel plate condenser, the energy is increased five times. The dielectric constant of the material is

Multiple choice

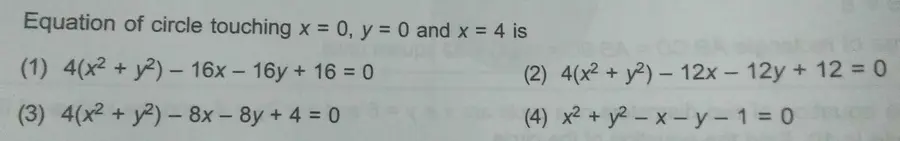
which gets rendered as:

Equation of circle touching

x = 0, y = 0

and

x = 4

is
(1)

4 (x^{2} + y^{2}) - 16 x - 16 y + 16 = 0

(2)

4 (x^{2} + y^{2}) - 12 x - 12 y + 12 = 0

(3)

4 (x^{2} + y^{2}) - 8 x - 8 y + 4 = 0

(4)

x^{2} + y^{2} - x - y - 1 = 0

Paragraphs and block mode math

Here’s a demo of v3/text working on multiple paragraphs:

Input image:

Text result:

The study of physical systems by means of particle simulations is well established
in a number of fields and is becoming increasingly important in others. The most classical example is probably celestial mechanics, but much recent work has been done in formulating and studying particle models in plasma physics, fluid dynamics, and molecular dynamics [ 5] Thee are two major classes of simulation methods. Dynamical simulations follow the trajectories of

N

particles over some time interval of interest. Given initial positions

{x_{t}}

and velocities, the trajectory of each particle is governed by Newton’s second law of motion:

m_{i} \frac{d^{2} x_{i}}{d t^{2}} = - \nabla_{i} Φ for i = 1, \dots, N

where

m_{i}

is the mass of

i

th particle and the force is obtained from the gradient of a potential function

Φ .

When one is interested in an equilibrium configuration of a set of particles rather than their time-dependent properties, an alternative approach is the Monte Carlo method. In this case, the potential function

Φ

has to be evaluated for a large number of configurations in an attempt to determine the potential minimum.

Newlines inside math to make text more legible

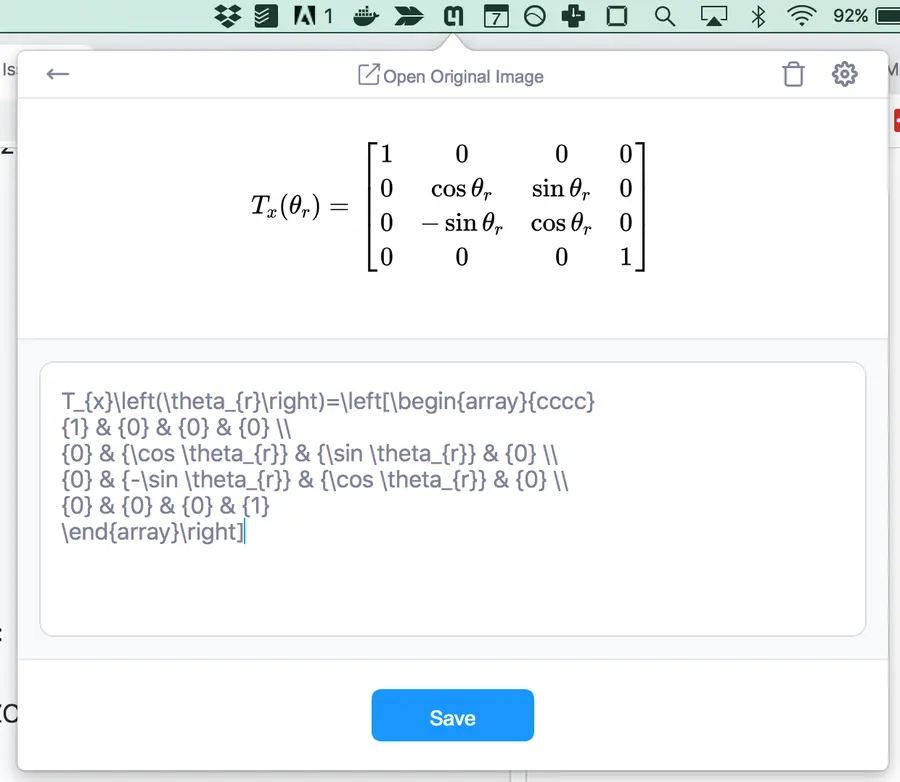
Conclusion

Questions or comments? Get in touch! nico@mathpix.com