[Note: outputs are rendered using mathpix-markdown-it]

Math and text

Request

{
    "src": "https://mathpix.com/examples/text_with_math_0.jpg",
    "formats": ["text", "html"],
    "data_options": {
        "include_asciimath": true,
        "include_latex": true
    }
}

request image

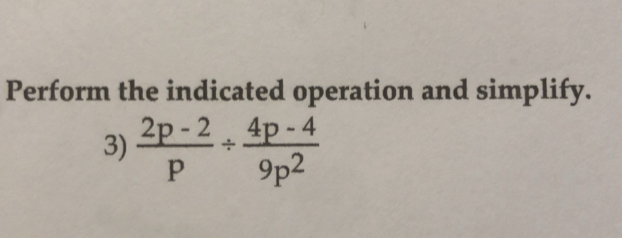
rendered(response.text)

Perform the indicated operation and simplify.
3)

\frac{2 p - 2}{p} \div \frac{4 p - 4}{9 p^{2}}

response

{
    "confidence": 0.9942260226265052,
    "confidence_rate": 0.9942999454546179,
    "data": [
        {
            "type": "asciimath",
            "value": "(2p-2)/(p)-:(4p-4)/(9p^(2))"
        },
        {
            "type": "latex",
            "value": "\\frac{2 p-2}{p} \\div \\frac{4 p-4}{9 p^{2}}"
        }
    ],
    "html": "<div>Perform the indicated operation and simplify.<br>\n3) <span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">(2p-2)/(p)-:(4p-4)/(9p^(2))</asciimath><latex style=\"display: none\">\\frac{2 p-2}{p} \\div \\frac{4 p-4}{9 p^{2}}</latex></span></div>\n",
    "text": "Perform the indicated operation and simplify.\n3) \\( \\frac{2 p-2}{p} \\div \\frac{4 p-4}{9 p^{2}} \\)"
}

response.html

<div>
   Perform the indicated operation and simplify.<br/>
   3) 
   <span class="math-inline ">
      <asciimath style="display: none;">(2p-2)/(p)-:(4p-4)/(9p^(2))</asciimath>
      <latex style="display: none">\frac{2 p-2}{p} \div \frac{4 p-4}{9 p^{2}}</latex>
   </span>
</div>

Full page of math and text

request

{
    "src": "https://mathpix.com/examples/full_page_with_math.jpg",
    "formats": ["text", "html"],
}

request image

rendered(response.text)

Insect Population Suppose that an insect population in millions is modeled by

f (x) = \frac{10 x + 1}{x + 1},

where

x \geq 0

is in months.
(a) Graph

f

in the window

[0, 14]

[0, 14]

. Find the equation of the horizontal asymptote.
(b) Determine the initial insect population.
(c) What happens to the population after several months?
(d) Interpret the horizontal asymptote.

Fish Population Suppose that the population of a species of fish in thousands is modeled by

f (x) = \frac{x + 10}{0.5 x^{2} + 1},

where

x \geq 0

is in years.
(a) Graph

f

in the window

[0, 12]

[0, 12]

. What is the equation of the horizontal asymptote?
(b) Determine the initial population.
(c) What happens to the population after many years?
(d) Interpret the horizontal asymptote.

response

{
    "auto_rotate_confidence": 5.960460924825384e-07,
    "auto_rotate_degrees": 0,
    "confidence": 0.9661174833308905,
    "confidence_rate": 0.9974907773474996,
    "html": "<ol start=\"73\">\n<li>Insect Population Suppose that an insect population in millions is modeled by</li>\n</ol>\n<div><span class=\"math-block \"></span></div>\n<div>where <span class=\"math-inline \"></span> is in months.<br>\n(a) Graph <span class=\"math-inline \"></span> in the window <span class=\"math-inline \"></span> by <span class=\"math-inline \"></span>. Find the equation of the horizontal asymptote.<br>\n(b) Determine the initial insect population.<br>\n(c) What happens to the population after several months?<br>\n(d) Interpret the horizontal asymptote.<br>\n74. Fish Population Suppose that the population of a species of fish in thousands is modeled by</div>\n<div><span class=\"math-block \"></span></div>\n<div>where <span class=\"math-inline \"></span> is in years.<br>\n(a) Graph <span class=\"math-inline \"></span> in the window <span class=\"math-inline \"></span> by <span class=\"math-inline \"></span>. What is the equation of the horizontal asymptote?<br>\n(b) Determine the initial population.<br>\n(c) What happens to the population after many years?<br>\n(d) Interpret the horizontal asymptote.</div>\n",
    "is_handwritten": false,
    "is_printed": true,
    "request_id": "2022_08_18_f696c599184c2e9ca986g",
    "text": "73. Insect Population Suppose that an insect population in millions is modeled by\n\\[\nf(x)=\\frac{10 x+1}{x+1},\n\\]\nwhere \\( x \\geq 0 \\) is in months.\n(a) Graph \\( f \\) in the window \\( [0,14] \\) by \\( [0,14] \\). Find the equation of the horizontal asymptote.\n(b) Determine the initial insect population.\n(c) What happens to the population after several months?\n(d) Interpret the horizontal asymptote.\n74. Fish Population Suppose that the population of a species of fish in thousands is modeled by\n\\[\nf(x)=\\frac{x+10}{0.5 x^{2}+1},\n\\]\nwhere \\( x \\geq 0 \\) is in years.\n(a) Graph \\( f \\) in the window \\( [0,12] \\) by \\( [0,12] \\). What is the equation of the horizontal asymptote?\n(b) Determine the initial population.\n(c) What happens to the population after many years?\n(d) Interpret the horizontal asymptote.",
    "version": "RSK-M102"
}

Handwritten text

request

{
    "src": "https://mathpix.com/examples/hw_text_0.jpg",
    "formats": ["text", "html"]
}

request image

rendered(response.text)

Machine learning
deep learning
computer vision
big data

response

{
    "confidence": 0.7723938592332265,
    "confidence_rate": 0.8613839302240724,
    "html": "<div>Powered by:</div>\n<ul>\n<li>Machine learning</li>\n<li>deep learning</li>\n<li>computer vision</li>\n<li>big data</li>\n</ul>\n",
    "text": "Powered by:\n- Machine learning\n- deep learning\n- computer vision\n- big data"
}

response.html

<div>
   <div>Powered by:</div>
   <ul>
      <li>Machine learning</li>
      <li>deep learning</li>
      <li>computer vision</li>
      <li>big data</li>
   </ul>
</div>

Handwritten text with spellcheck

Spellcheck can make a big difference in accuracy on handwritten content. See here for an example of the output without spellcheck, and then with spellcheck.

request image

request without spellcheck

{
    "src": "https://mathpix-ocr-examples.s3.amazonaws.com/hw_correction_0.jpg",
}

request with spellcheck

{
    "src": "https://mathpix-ocr-examples.s3.amazonaws.com/hw_correction_0.jpg",
    "enable_spell_check": true
}

rendered(response.text) without spellcheck

Dolution:
Ans 24). In developing a chart to flot a course of action, with many of the events or milestones, we will we Process deciscon pirogram chart.
so, optison (A) is cossect ansuver.

rendered(response.text) with spellcheck

Solution:
Ans 24). In developing a chart to plot a course of action, with many of the events or milestones, we will we Process decision program chart.
so, option (A) is correct answer.

Advanced math fonts

We support: \mathscr, \mathcal, \mathfrak, \mathbb, \boldsymbol, \mathrm

request

{
    "src": "https://mathpix.com/examples/math_fonts_0.jpg",
    "formats": ["text", "html", "data"],
    "data_options": {
        "include_mathml": true,
        "include_asciimath": true,
    }
}

request image

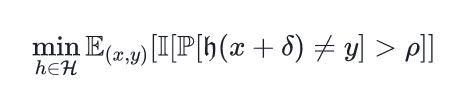
rendered(response.text)

min_{h \in H} E_{(x, y)} [I [P [h (x + δ) \neq y] > ρ]]

response

{
    "auto_rotate_confidence": 2.0265538154262686e-06,
    "auto_rotate_degrees": 0,
    "confidence": 1,
    "confidence_rate": 1,
    "data": [
        {
            "type": "mathml",
            "value": "<math xmlns=\"http://www.w3.org/1998/Math/MathML\">\n  <munder>\n    <mo data-mjx-texclass=\"OP\" movablelimits=\"true\">min</mo>\n    <mrow>\n      <mi>h</mi>\n      <mo>\u2208</mo>\n      <mrow>\n        <mi data-mjx-variant=\"-tex-calligraphic\" mathvariant=\"script\">H</mi>\n      </mrow>\n    </mrow>\n  </munder>\n  <msub>\n    <mrow>\n      <mi mathvariant=\"double-struck\">E</mi>\n    </mrow>\n    <mrow>\n      <mo stretchy=\"false\">(</mo>\n      <mi>x</mi>\n      <mo>,</mo>\n      <mi>y</mi>\n      <mo stretchy=\"false\">)</mo>\n    </mrow>\n  </msub>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"double-struck\">I</mi>\n  </mrow>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"double-struck\">P</mi>\n  </mrow>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"fraktur\">h</mi>\n  </mrow>\n  <mo stretchy=\"false\">(</mo>\n  <mi>x</mi>\n  <mo>+</mo>\n  <mi>\u03b4</mi>\n  <mo stretchy=\"false\">)</mo>\n  <mo>\u2260</mo>\n  <mi>y</mi>\n  <mo stretchy=\"false\">]</mo>\n  <mo>&gt;</mo>\n  <mi>\u03c1</mi>\n  <mo stretchy=\"false\">]</mo>\n  <mo stretchy=\"false\">]</mo>\n</math>"
        },
        {
            "type": "asciimath",
            "value": "min_(h inH)E_((x,y))[I[P[h(x+delta)!=y] > rho]]"
        }
    ],
    "html": "<div><span class=\"math-inline \"><mathml style=\"display: none\"><math xmlns=\"http://www.w3.org/1998/Math/MathML\">\n  <munder>\n    <mo data-mjx-texclass=\"OP\" movablelimits=\"true\">min</mo>\n    <mrow>\n      <mi>h</mi>\n      <mo>&#x2208;</mo>\n      <mrow>\n        <mi data-mjx-variant=\"-tex-calligraphic\" mathvariant=\"script\">H</mi>\n      </mrow>\n    </mrow>\n  </munder>\n  <msub>\n    <mrow>\n      <mi mathvariant=\"double-struck\">E</mi>\n    </mrow>\n    <mrow>\n      <mo stretchy=\"false\">(</mo>\n      <mi>x</mi>\n      <mo>,</mo>\n      <mi>y</mi>\n      <mo stretchy=\"false\">)</mo>\n    </mrow>\n  </msub>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"double-struck\">I</mi>\n  </mrow>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"double-struck\">P</mi>\n  </mrow>\n  <mo stretchy=\"false\">[</mo>\n  <mrow>\n    <mi mathvariant=\"fraktur\">h</mi>\n  </mrow>\n  <mo stretchy=\"false\">(</mo>\n  <mi>x</mi>\n  <mo>+</mo>\n  <mi>&#x3B4;</mi>\n  <mo stretchy=\"false\">)</mo>\n  <mo>&#x2260;</mo>\n  <mi>y</mi>\n  <mo stretchy=\"false\">]</mo>\n  <mo>&gt;</mo>\n  <mi>&#x3C1;</mi>\n  <mo stretchy=\"false\">]</mo>\n  <mo stretchy=\"false\">]</mo>\n</math></mathml><asciimath style=\"display: none;\">min_(h inH)E_((x,y))[I[P[h(x+delta)!=y] &gt; rho]]</asciimath></span></div>\n",
    "is_handwritten": false,
    "is_printed": true,
    "request_id": "2022_08_18_fb4bd52cff1c80f9f09fg",
    "text": "\\( \\min _{h \\in \\mathcal{H}} \\mathbb{E}_{(x, y)}[\\mathbb{I}[\\mathbb{P}[\\mathfrak{h}(x+\\delta) \\neq y]>\\rho]] \\)",
    "version": "RSK-M102"
}

Multiple choice question

request

{
    "src": "https://mathpix.com/examples/multiple_choice_0.png",
    "formats": ["text", "data", "html"],
    "data_options": {
        "include_asciimath": true
    }
}

request image

rendered(response.text)

$z_{1}$ and $z_{2}$ are unimodular complex numbers that satisfy $z_{1}^{2} + z_{2}^{2} = 4$ then the value of $\frac{{(z_{1} + {\bar{z}}_{1})}^{2} + {(z_{2} + {\bar{z}}_{2})}^{2}}{2}$ is
(a) 10
(b) 11
(c) 12
(d) 13

response.json

{
    "confidence": 0.9110662494831634,
    "confidence_rate": 0.9488863482674147,
    "data": [
        {
            "type": "asciimath",
            "value": "z_(1)"
        },
        {
            "type": "asciimath",
            "value": "z_(2)"
        },
        {
            "type": "asciimath",
            "value": "z_(1)^(2)+z_(2)^(2)=4"
        },
        {
            "type": "asciimath",
            "value": "((z_(1)+ bar(z)_(1))^(2)+(z_(2)+ bar(z)_(2))^(2))/(2)"
        }
    ],
    "html": "<ol start=\"11\">\n<li><span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">z_(1)</asciimath></span> and <span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">z_(2)</asciimath></span> are unimodular complex numbers that satisfy <span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">z_(1)^(2)+z_(2)^(2)=4</asciimath></span> then the value of <span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">((z_(1)+ bar(z)_(1))^(2)+(z_(2)+ bar(z)_(2))^(2))/(2)</asciimath></span> is<br>\n(a) 10<br>\n(b) 11<br>\n\u00a9 12<br>\n(d) 13</li>\n</ol>\n",
    "text": "11. \\( z_{1} \\) and \\( z_{2} \\) are unimodular complex numbers that satisfy \\( z_{1}^{2}+z_{2}^{2}=4 \\) then the value of \\( \\frac{\\left(z_{1}+\\bar{z}_{1}\\right)^{2}+\\left(z_{2}+\\bar{z}_{2}\\right)^{2}}{2} \\) is\n(a) 10\n(b) 11\n(c) 12\n(d) 13"
}

response.text

11. \( z_{1} \) and \( z_{2} \) are unimodular complex numbers that satisfy \( z_{1}^{2}+z_{2}^{2}=4 \) then the value of \( \frac{\left(z_{1}+\bar{z}_{1}\right)^{2}+\left(z_{2}+\bar{z}_{2}\right)^{2}}{2} \) is
(a) 10
(b) 11
(c) 12
(d) 13

response.html

<ol start="11">
   <li>
      <span class="math-inline ">
         <asciimath style="display: none;">z_(1)</asciimath>
         <latex style="display: none">z_{1}</latex>
      </span>
      and 
      <span class="math-inline ">
         <asciimath style="display: none;">z_(2)</asciimath>
         <latex style="display: none">z_{2}</latex>
      </span>
      are unimodular complex numbers that satisfy 
      <span class="math-inline ">
         <asciimath style="display: none;">z_(1)^(2)+z_(2)^(2)=4</asciimath>
         <latex style="display: none">z_{1}^{2}+z_{2}^{2}=4</latex>
      </span>
      then the value of 
      <span class="math-inline ">
         <asciimath style="display: none;">((z_(1)+ bar(z)_(1))^(2)+(z_(2)+ bar(z)_(2))^(2))/(2)</asciimath>
         <latex style="display: none">\frac{\left(z_{1}+\bar{z}_{1}\right)^{2}+\left(z_{2}+\bar{z}_{2}\right)^{2}}{2}</latex>
      </span>
      is<br/>
      (a) 10<br/>
      (b) 11<br/>
      (c) 12<br/>
      (d) 13
   </li>
</ol>

Standalone equation

request

{
    "src": "https://mathpix.com/examples/limit.jpg",
    "formats": ["text", "data", "html"],
    "data_options": {
        "include_asciimath": true,
        "include_latex": true
    }
}

request image

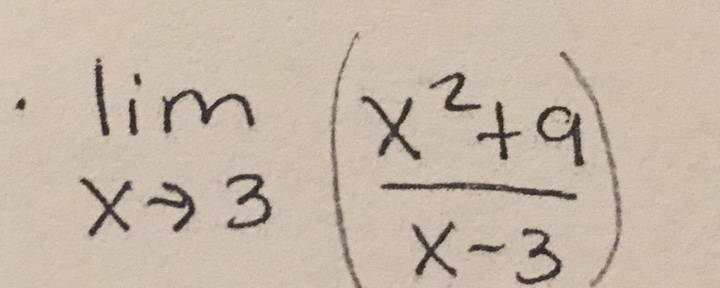
rendered(response.text)

lim_{x \to 3} (\frac{x^{2} + 9}{x - 3})

response

{
    "confidence": 0.9982182085336344,
    "confidence_rate": 0.9982182085336344,
    "data": [
        {
            "type": "asciimath",
            "value": "lim_(x rarr3)((x^(2)+9)/(x-3))"
        },
        {
            "type": "latex",
            "value": "\\lim _{x \\rightarrow 3}\\left(\\frac{x^{2}+9}{x-3}\\right)"
        }
    ],
    "html": "<div><span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">lim_(x rarr3)((x^(2)+9)/(x-3))</asciimath><latex style=\"display: none\">\\lim _{x \\rightarrow 3}\\left(\\frac{x^{2}+9}{x-3}\\right)</latex></span></div>\n",
    "text": "\\( \\lim _{x \\rightarrow 3}\\left(\\frac{x^{2}+9}{x-3}\\right) \\)"
}

Block mode math

Block mode math when mixed with text is represented using \[ ... \] delimiters.

request

{
    "src": "https://mathpix.com/examples/block_math_0.jpg",
}

request image

rendered(response.text)

We first verify the result for

X = I_{A}

(indicator function) where

A \in G .

In this case

\begin{aligned} \int_{B} I_{A} E (Y ∣ G) d P & = \int_{A \cap B} E (Y ∣ G) d P \\ = \int_{A \cap B} Y d P \\ = \int_{B} I_{A} Y d P \end{aligned}

response

{
    "request_id": "595ec0b9deda512b4d4582a86a040d14",
    "is_printed": true,
    "is_handwritten": false,
    "auto_rotate_confidence": 0.0004953074438702743,
    "auto_rotate_degrees": 0,
    "confidence": 0.5302130355194095,
    "confidence_rate": 0.7655196701192286,
    "text": "We first verify the result for \\( X=\\mathbb{I}_{A} \\) (indicator function) where \\( A \\in \\mathscr{G} . \\) In this case\n\\[\n\\begin{aligned}\n\\int_{B} \\mathbb{I}_{A} E(Y \\mid \\mathscr{G}) d \\mathbb{P} &=\\int_{A \\cap B} E(Y \\mid \\mathscr{G}) d \\mathbb{P} \\\\\n&=\\int_{A \\cap B} Y d \\mathbb{P} \\\\\n&=\\int_{B} \\mathbb{I}_{A} Y d \\mathbb{P}\n\\end{aligned}\n\\]"
}

Long division

In LaTeX, we represent long division using a special \longdiv character. This is the only non standard LaTeX character we emit. Note that we convert long divisions to normal division for asciimath, which is a computation centric math language, whereas LaTeX is more visually focused.

We render \longdiv in Mathpix Markdown using the following MathJax macro: \overline{\smash{)}#1}. You can render this in PdfLaTeX by adding \newcommand\longdiv[1]{\overline{\smash{)}#1}} to your preamble.

request

{
    "src": "https://mathpix.com/examples/long_division.jpg",
    "formats": ["text"],
}

request image

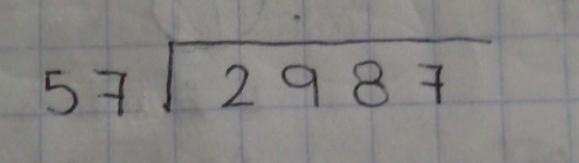
rendered(response.text)

572987

response

{
    "auto_rotate_confidence": 0,
    "auto_rotate_degrees": 0,
    "confidence": 1,
    "confidence_rate": 1,
    "is_handwritten": true,
    "is_printed": false,
    "request_id": "2022_08_18_e4b5c809bf47b46d4f59g",
    "text": "\\( 5 7 \\longdiv { 2 9 8 7 } \\)",
    "version": "RSK-M101"
}

System of equations

request

{
    "src": "https://mathpix.com/examples/equation_system_0.jpg",
    "formats": ["text", "data", "html"],
    "data_options": {
        "include_asciimath": true,
        "include_latex": true
    }
}

request image

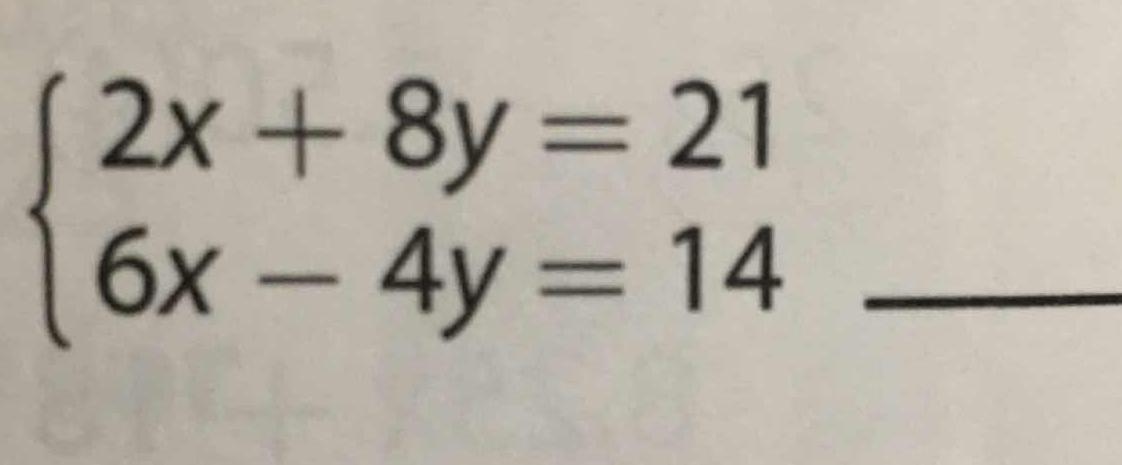
rendered(response.text)

{\begin{cases} 2 x + 8 y = 21 \\ 6 x - 4 y = 14 \end{cases}

response

{
    "confidence": 0.9960272582188906,
    "confidence_rate": 0.9960272582188906,
    "data": [
        {
            "type": "asciimath",
            "value": "{[2x+8y=21],[6x-4y=14]:}"
        },
        {
            "type": "latex",
            "value": "\\left\\{\\begin{array}{l}2 x+8 y=21 \\\\ 6 x-4 y=14\\end{array}\\right."
        }
    ],
    "html": "<div><span  class=\"math-inline \" >\n<asciimath style=\"display: none;\">{[2x+8y=21],[6x-4y=14]:}</asciimath><latex style=\"display: none\">\\left\\{\\begin{array}{l}2 x+8 y=21 \\\\ 6 x-4 y=14\\end{array}\\right.</latex></span></div>\n",
    "text": "\\( \\left\\{\\begin{array}{l}2 x+8 y=21 \\\\ 6 x-4 y=14\\end{array}\\right. \\)"
}

response.html

<div>
   <span class="math-inline ">
      <asciimath style="display: none;">{[2x+8y=21],[6x-4y=14]:}</asciimath>
      <latex style="display: none">\left\{\begin{array}{l}2 x+8 y=21 \\ 6 x-4 y=14\end{array}\right.</latex>
   </span>
</div>

Digital ink (math)

request

POST v3/strokes

{
    "strokes": {
        "strokes": {
            "x":[[33,34,36,45,50,58,59,61],[65,65,64,63,60,57,51,49,46,45,44,42,42,41],[82,83,84,87,89,92,93,93,94,94,95,95,96,96],[82,82,82,83,84,88,93,98,101,102],[130,130,134,139,147,149,150],[179,179,176,175,170,167,165,164,164,163,163,164,165,172,176,184,187,190,192,193,195,196,197,198,198,198,196,195,191,178,174,172,171],[245,245,245,244,244,243,243,243,243,243,243,243,243],[228,228,233,238,248,256,257,258],[231,234,239,253,258,266,268],[284,285,285,290,294,301,303,304,304,305,306,306,308,311,317,321,326,328,332,333,337,340,347,352,372,388,428,478,506,531,564,569],[370,370,369,363,361,355,353,350,350,350,350,351,354,362,364,367,367,371,372,373,374,374,374,374,372,365,362,355,354,352,352,351,351,351,350],[396,397,397,398,399,399,402,404,405,405,406,406,406,403,400,397,392,392,391,391,391,393,401,406,411,420,420,421],[433,434,434,434,435,442,447,455,458,459],[484,484,484,483,481,480,477,476,474,474,474,474,474,474,474,475,478,481,490,495,501,503,504,504,505,505,505],[497,496,496,496,496,496,496,496,496,497,497,497,497,497,497,498],[527,528,527,525,522,520,518,517,517,517,517,517,517,518,518,519,520,521,523,526,526,528,529,530,530,530,530,530,530,530,530,532,534,536,537,538,541,542,545,546,547,548],[565,565,565,565,564,562,558,556,555,554,553,553,553,553,553,554,554,556,556,559,561,566,567,568,569,570,571,572,573,573,574,574],[124,126,129,148,164,198,231,243,266,278,304,319,347,359,383,394,414,425,449,461,473,494,502,516,523,533,538,543,544,547,548,550,551,553,553,553,554,554,554,555,556,558,560,567,572,580,582,582],[289,289,290,291,293,301,308,318,320,322,323,324,325,326,326,326,325,322,316,307,304,297,296,293,293,292,292,291,291,291,293,296,307,310,315,316,318,318,321,322,325,327,329,330],[360,360,360,356,355,351,341,338,335,334,334,335,337,340,341,342,344,344,347,348,350,351,352,353,353,353,353,353,353,353,353,354,355,356,357,357,358,358,358,358,358,358,358,358,358,358,358,358,358,358,358,358,358,358,357,357,357,357,357,357,357,357,357,357,358,360,362,364,365,366,369,378,381,382,383,384]],
            "y":[[188,190,194,207,214,224,227,229],[192,192,194,196,201,205,214,217,222,224,227,228,230,230],[201,201,201,202,203,203,203,203,203,203,203,203,203,203],[218,219,219,219,220,220,221,221,221,221],[171,170,169,168,167,167,167],[129,130,144,154,178,195,202,207,209,210,210,208,207,199,195,190,188,188,188,188,189,191,193,196,197,200,201,201,202,202,202,202,202],[143,144,146,149,158,163,169,171,172,173,174,174,175],[166,166,165,164,164,164,164,164],[191,191,191,191,191,191,191],[167,167,168,187,197,213,216,218,218,218,218,217,214,209,193,185,166,156,140,135,127,123,116,113,109,107,106,106,106,104,103,102],[154,156,159,172,179,195,202,206,207,208,207,206,204,200,200,200,200,201,203,206,207,208,209,210,211,211,211,211,211,211,210,210,209,208,208],[152,152,151,151,150,149,148,148,148,148,148,149,152,162,166,170,175,176,176,177,177,178,180,180,181,181,181,181],[194,195,195,195,195,194,193,193,192,192],[153,153,155,158,170,175,185,190,197,199,201,202,202,203,203,204,205,205,205,205,205,205,205,205,204,204,204],[190,192,194,200,204,209,210,212,212,214,214,215,215,216,217,217],[193,192,192,192,192,193,194,195,197,199,201,203,203,205,206,207,207,207,207,207,207,206,206,201,199,196,195,194,194,194,196,199,202,205,206,207,208,209,210,210,211,211],[190,190,190,189,189,189,189,190,190,191,192,194,195,197,198,199,200,202,203,204,205,206,206,207,207,207,207,207,207,207,206,206],[228,228,228,228,228,228,231,231,231,231,232,234,234,234,235,235,235,236,236,236,238,239,239,240,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241,241],[269,269,269,268,267,263,261,259,259,259,259,259,262,263,265,268,269,273,279,284,285,288,288,289,289,289,289,289,289,289,288,288,288,290,293,294,295,296,296,296,296,295,294,294],[278,278,278,277,277,277,277,277,278,279,282,286,290,293,294,294,295,295,295,295,294,294,293,292,291,290,289,288,288,288,288,288,289,290,291,291,291,290,288,288,287,286,286,286,285,285,284,284,284,283,283,282,282,282,281,281,280,280,279,279,279,278,279,280,282,287,290,293,295,296,297,299,300,300,300,300]]
        }
    },
    "formats": ["text", "html"],
    "data_options": {
        "include_latex": true
    }
}

request strokes visualization

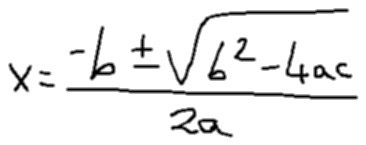
rendered(response.text)

x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

response

{
    "confidence": 0.997059396020232,
    "confidence_rate": 0.997059396020232,
    "html": "<div><span  class=\"math-inline \" >\n<latex style=\"display: none\">x=\\frac{-b \\pm \\sqrt{b^{2}-4 a c}}{2 a}</latex></span></div>\n",
    "text": "\\( x=\\frac{-b \\pm \\sqrt{b^{2}-4 a c}}{2 a} \\)"
}

response.html

<div>
    <span  class=\"math-inline \" >
        <latex style=\"display: none\">x=\\frac{-b \\pm \\sqrt{b^{2}-4 a c}}{2 a}</latex>
    </span>
</div>

request

{
    "strokes": {
        "strokes": {
            "x":[[94,94,94,95,97,98,104,107,113,117,125,134,138,140,143,144,144,143,143,143,144,145,146,149,150,151,151,151,150,149,148,147,145,142,135,132,129,129,130,130,134,137,142,142,143,144,144],[187,187,187,189,192,201,202,205,205,206,206],[185,187,190,192,193,195,196,198,199,201,202,203],[251,251,251,251,251,251,251,251,251,251,251,251,251,251,252,253,258,263,270,276,282,283,284,284,284,284,284,283,283,282,281,281,282,283,288,289,296,297,301,303,306,307,308,309,309,309,309,309,309,309,309],[321,325,334,342,358,366,378,380,380],[365,364,363,359,356,352,347,343,342,341,339,338,337,337,336,336,336,335,335,335,335,335,334,334,333,333,333,332,332,332],[443,444,444,444,444,444,445,445,447,447,448,448,448],[423,423,425,430,441,448,464,467,468,469,469,470,470],[510,510,511,511,512,512,513,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,514,513,513,513,513,513,513,513,513,513,514,515,515,516,517,519,523,528,529,531,534,540,542,543,544,545,546,546,549,549,551,552,553,554,554,554,554,555,555,555,555,555,554,554,553,553,552,551,550,549,548,547,546,544,541,540,538,535,533,530,529,527,526,523,523,522,521,520,520,519,518,518,518,517,517,516,516,515,515,515,514,514,514],[121,121,122,130,136,148,154,162,163,164],[174,174,172,168,158,154,141,137,129,126,125,124],[216,217,225,232,246,251,256,257],[219,219,221,227,232,243,246,247,249,249,251,252,255,257,260,261,261],[320,320,320,320,321,323,324,325,326,327,329,335,339,345,347,350,352,352,354,354,354,354,354,353,353,353,352,352,352,352,352,352,353,356,358,361,362,362,363,364,364,364,364,364,364,364,364,364,364,363,363,363,361,361,359,358,355,355,353,352,351,351,350,350,349,349,349,349,349,350,351,356,358,361,361],[377,378,379,381,387,390,393,394,395,395,397,397,398,398,394,391,382,377,371,368,366,365,365,364,364,364,366,368,375,378,384,388,391,394,398,408,413,421,422,423,423],[445,445,446,447,454,457,464,467,470,472,473,474,474,475,476],[519,519,520,525,529,534,535,536,536,536,537,537,537,537,537,537,537,537,538,538,538,539,539,539,540,540,540]],
            "y":[[75,76,79,82,87,91,100,102,106,107,107,104,101,98,92,88,83,80,78,79,84,92,103,115,127,147,159,164,171,172,173,173,173,170,160,156,151,150,149,148,148,148,148,148,148,148,147],[88,88,88,88,88,88,88,88,88,88,88],[110,110,110,110,110,110,110,110,110,111,111,111],[89,89,99,104,118,123,126,127,126,116,102,97,91,89,87,87,87,87,90,95,104,107,114,115,117,118,118,118,118,114,109,99,93,90,84,83,81,81,82,84,91,96,106,110,113,114,116,117,119,119,119],[85,87,94,101,115,121,129,130,131],[84,84,85,89,91,94,101,106,108,110,112,113,115,116,116,117,118,118,119,119,120,120,121,121,122,122,123,123,124,124],[80,80,81,82,87,90,95,98,105,108,115,116,117],[98,98,98,98,98,98,98,98,98,98,98,98,98],[40,41,42,44,52,57,71,76,86,89,94,98,101,104,107,108,109,110,111,111,113,113,114,114,114,115,115,116,117,118,118,117,117,115,114,112,110,108,107,106,105,105,104,102,101,101,101,101,100,100,100,100,100,101,101,102,103,104,104,105,106,106,107,109,109,110,111,112,113,115,117,118,119,120,121,122,122,123,123,123,123,123,123,123,123,122,121,121,121,120,119,119,119,119,118,118,118,117,117,117,117,117,117,117,117,117,117,117,117,117],[285,286,288,299,306,321,327,334,335,335],[290,290,292,296,304,308,321,329,339,343,346,346],[305,304,304,304,304,304,304,304],[334,334,334,334,334,334,334,334,334,334,334,334,334,334,334,334,334],[295,297,300,307,310,317,320,323,324,326,326,327,327,327,327,326,325,324,322,320,315,314,311,309,308,307,307,306,306,307,310,317,324,339,346,358,361,363,367,367,370,370,372,372,373,374,375,376,377,378,378,379,380,380,380,380,381,381,382,382,382,382,381,381,378,377,375,373,371,369,368,366,365,364,364],[259,258,256,254,250,248,247,247,247,247,248,249,256,261,271,276,286,289,293,294,294,294,294,293,292,291,290,290,290,291,294,296,297,297,297,294,292,290,289,289,289],[313,313,312,312,312,312,312,312,312,312,312,312,312,312,312],[292,292,290,285,281,275,272,270,269,270,273,278,290,297,309,316,326,331,335,336,337,337,338,339,342,343,345]]
        }
    },
    "formats": ["text", "html"],
    "data_options": {
        "include_latex": true
    }
}

request strokes visualization

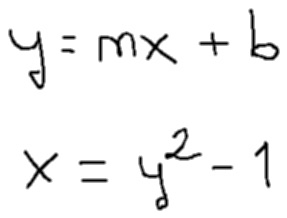
rendered(response.text)

\begin{array}{l} y = m x + b \\ x = y^{2} - 1 \end{array}

response

{
    "confidence": 1,
    "confidence_rate": 1,
    "html": "<div><span class=\"math-inline \">\n<latex style=\"display: none\">\\begin{array}{l}y=m x+b \\\\ x=y^{2}-1\\end{array}</latex></span></div>\n",
    "text": "\\( \\begin{array}{l}y=m x+b \\\\ x=y^{2}-1\\end{array} \\)"
}

response.html

<div>
   <span class="math-inline ">
      <latex style="display: none">\begin{array}{l}y=m x+b \\ x=y^{2}-1\end{array}</latex>
   </span>
</div>

Tables

request

{
    "src": "https://mathpix.com/examples/table_simple_0.jpg",
    "formats": ["text", "data", "html"],
    "data_options": {
        "include_tsv": true,
        "include_table_html": true,
        "include_latex": true
    }
}

request image

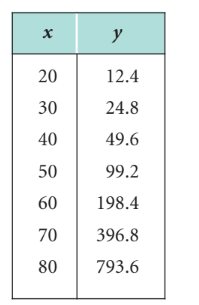
rendered(response.text)

$x$	$y$
20	12.4
30	24.8
40	49.6
50	99.2
60	198.4
70	396.8
80	793.6

response

{
    "confidence": 0.6581662076606053,
    "confidence_rate": 0.6581662076606053,
    "data": [
        {
            "type": "html",
            "value": "<table id=\"tabular\">\n<tbody>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-b
ottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; \"><span class=\"math-inline \">\n<latex style=\"display: none\">x</latex></span></td>\n<td style=\"text-align: center; border-right-style: sol
id !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; \"><span class=\"math-inline \">\n<latex style=\"display: none\">y</latex></span></td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !im
portant; width: auto; vertical-align: middle; \">20</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">12.4</td>\n</tr>\n<tr style=\"border-top: none !impor
tant; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">30</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">24.8</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td
style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">40</td>\n<td style=\"text-align: center; bo
rder-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">49.6</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style:
 solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">50</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-rig
ht-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">99.2</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !imp
ortant; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">60</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none
!important; border-top: none !important; width: auto; vertical-align: middle; \">198.4</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important;
 border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">70</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; widt
h: auto; vertical-align: middle; \">396.8</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-b
ottom-style: solid !important; border-bottom-width: 1px !important; border-top: none !important; width: auto; vertical-align: middle; \">80</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !i
mportant; border-top: none !important; width: auto; vertical-align: middle; \">793.6</td>\n</tr>\n</tbody>\n</table>"
        },
        {
            "type": "tsv",
            "value": "\\( x \\)\t\\( y \\)\n20\t12.4\n30\t24.8\n40\t49.6\n50\t99.2\n60\t198.4\n70\t396.8\n80\t793.6"
        },
        {
            "type": "latex",
            "value": "x"
        },
        {
            "type": "latex",
            "value": "y"
        }
    ],
    "html": "<div class=\"table_tabular \" style=\"text-align: center\">\n<table id=\"tabular\">\n<tbody>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !imp
ortant; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; \"><span  class=\"math-inline \" >\n<latex style=\"display: none\">x</latex></span></td>\n<
td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; \"><span  class=\"math-inline
\" >\n<latex style=\"display: none\">y</latex></span></td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">20</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle;
\">12.4</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top
: none !important; width: auto; vertical-align: middle; \">30</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">24.8</td>\n</tr>\n<tr style=\"border-top: n
one !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align
: middle; \">40</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">49.6</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important
;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">50</td>\n<td style=\"text-align:
center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">99.2</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-l
eft-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">60</td>\n<td style=\"text-align: center; border-right-style: solid !important;
border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">198.4</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-widt
h: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">70</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bo
ttom: none !important; border-top: none !important; width: auto; vertical-align: middle; \">396.8</td>\n</tr>\n<tr style=\"border-top: none !important; border-bottom: none !important;\">\n<td style=\"text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid
!important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top: none !important; width: auto; vertical-align: middle; \">80</td>\n<td style=\"text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bot
tom-style: solid !important; border-bottom-width: 1px !important; border-top: none !important; width: auto; vertical-align: middle; \">793.6</td>\n</tr>\n</tbody>\n</table>\n<tsv style=\"display: none\">\\( x \\)\t\\( y \\)\n20\t12.4\n30\t24.8\n40\t49.6\n50\t99.2\n60\t198.4\n70\t396.8\n80\t793.6</tsv></div>\n",
    "text": "\\begin{tabular}{|c|c|}\n\\hline\\( x \\) & \\( y \\) \\\\\n\\hline 20 & 12.4 \\\\\n30 & 24.8 \\\\\n40 & 49.6 \\\\\n50 & 99.2 \\\\\n60 & 198.4 \\\\\n70 & 396.8 \\\\\n80 & 793.6 \\\\\n\\hline\n\\end{tabular}"
}

response.html

<div class="table_tabular " style="text-align: center">
   <table id="tabular">
      <tbody>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; ">
               <span  class="math-inline " >
                  <latex style="display: none">x</latex>
               </span>
            </td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top-style: solid !important; border-top-width: 1px !important; width: auto; vertical-align: middle; ">
               <span  class="math-inline " >
                  <latex style="display: none">y</latex>
               </span>
            </td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">20</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">12.4</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">30</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">24.8</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">40</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">49.6</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">50</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">99.2</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">60</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">198.4</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">70</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom: none !important; border-top: none !important; width: auto; vertical-align: middle; ">396.8</td>
         </tr>
         <tr style="border-top: none !important; border-bottom: none !important;">
            <td style="text-align: center; border-left-style: solid !important; border-left-width: 1px !important; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top: none !important; width: auto; vertical-align: middle; ">80</td>
            <td style="text-align: center; border-right-style: solid !important; border-right-width: 1px !important; border-bottom-style: solid !important; border-bottom-width: 1px !important; border-top: none !important; width: auto; vertical-align: middle; ">793.6</td>
         </tr>
      </tbody>
   </table>
   <tsv style="display: none">\( x \)      \( y \)
      20      12.4
      30      24.8
      40      49.6
      50      99.2
      60      198.4
      70      396.8
      80      793.6
   </tsv>
</div>

response.data[1].value

\( x \) \( y \)
20      12.4
30      24.8
40      49.6
50      99.2
60      198.4
70      396.8
80      793.6

Diagrams

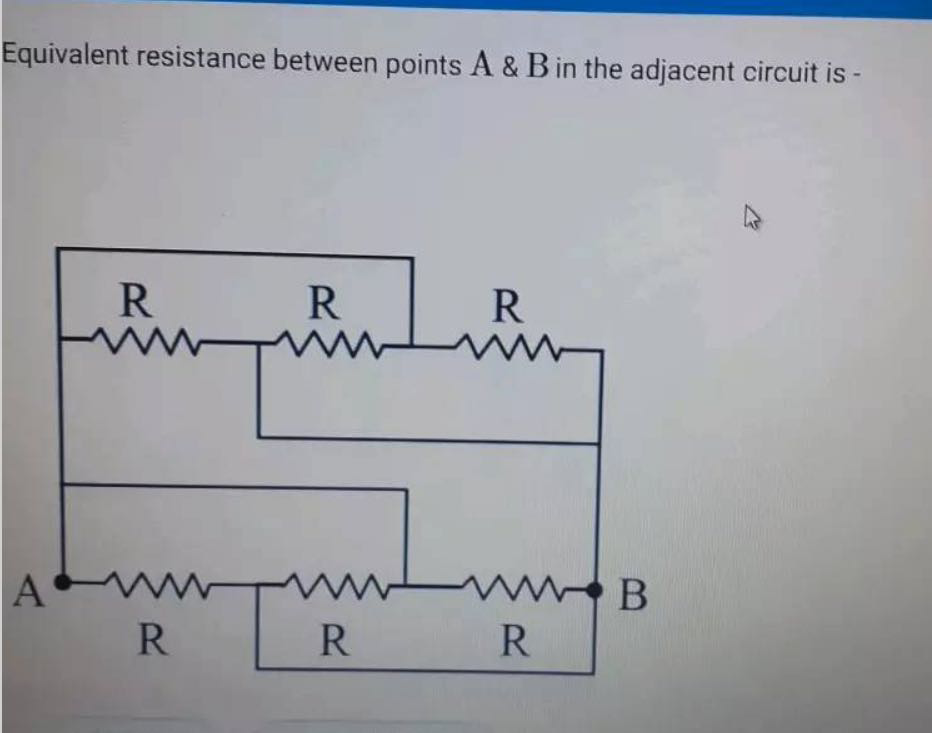
Diagrams are localized and included in line_data but do not generate OCR results.

request

{
    "src": "https://mathpix.com/examples/text_with_diagram.png",
    "formats": ["html"],
    "include_line_data": true,
    "data_options": {
        "include_asciimath": true,
        "include_mathml": true
    }
}

request image

response

{
    "confidence": 0.651358435330524,
    "confidence_rate": 0.651358435330524,
    "html": "<div>Equivalent resistance between points <span class=\"math-inline \"><mathml style=\"display: none\"><math xmlns=\"http://www.w3.org/1998/Math/MathML\">\n  <mrow>\n    <mi mathvariant=\"normal\">A</mi>\n  </mrow>\n  <mi mathvariant=\"normal\">&amp;</mi>\n  <mrow>\n    <mi mathvariant=\"normal\">B</mi>\n  </mrow>\n</math></mathml><asciimath style=\"display: none;\">A&amp;B</asciimath></span> in the adjacent circuit is</div>\n",
    "line_data": [
        {
            "type": "text",
            "cnt": [
                [
                    859,
                    81
                ],
                [
                    739,
                    91
                ],
                [
                    626,
                    91
                ],
                [
                    -2,
                    66
                ],
                [
                    0,
                    34
                ],
                [
                    739,
                    52
                ],
                [
                    859,
                    63
                ]
            ],
            "included": true,
            "text": "Equivalent resistance between points \\( \\mathrm{A} \\& \\mathrm{B} \\) in the adjacent circuit is",
            "after_hyphen": false,
            "confidence": 0.651358435330524,
            "confidence_rate": 0.9948483133235457,
            "html": "<div>Equivalent resistance between points <span class=\"math-inline \"><mathml style=\"display: none\"><math xmlns=\"http://www.w3.org/1998/Math/MathML\">\n  <mrow>\n    <mi mathvariant=\"normal\">A</mi>\n  </mrow>\n  <mi mathvariant=\"normal\">&amp;</mi>\n  <mrow>\n    <mi mathvariant=\"normal\">B</mi>\n  </mrow>\n</math></mathml><asciimath style=\"display: none;\">A&amp;B</asciimath></span> in the adjacent circuit is</div>\n"
        },
        {
            "type": "diagram",
            "cnt": [
                [
                    654,
                    244
                ],
                [
                    651,
                    683
                ],
                [
                    7,
                    678
                ],
                [
                    11,
                    238
                ]
            ],
            "included": false,
            "error_id": "image_not_supported"
        }
    ]
}

rendered(response.text)

Equivalent resistance between points

A & B

in the adjacent circuit is

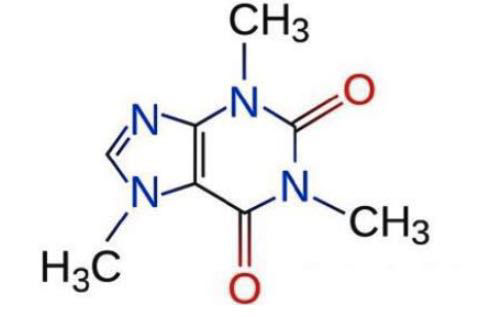
Chemistry diagrams

Chemistry diagrams are treated just like other diagrams, except they also include a text field subtype in line_data which is equal to chemistry (see here for docs).

Like diagrams, they do not generate OCR results at the present time, unless you enable experimental chemistry OCR support via the include_smiles parameter (see next section).

request

{
    "src": "https://mathpix.com/examples/chemistry_caffeine.png",
    "include_line_data": true
}

request image

response

{
    "is_printed": true,
    "is_handwritten": false,
    "error": "Content not found",
    "error_info": {
        "id": "image_no_content",
        "message": "Content not found"
    },
    "line_data": [
        {
            "type": "diagram",
            "cnt": [
                [
                    434,
                    306
                ],
                [
                    27,
                    306
                ],
                [
                    27,
                    -2
                ],
                [
                    434,
                    0
                ]
            ],
            "included": false,
            "subtype": "chemistry",
            "error_id": "image_not_supported"
        }
    ]
}

Chemistry diagram OCR

To enable experimental chemistry diagram OCR, simply include the include_smiles parameter in the body of the request. The Mathpix Markdown syntax <smiles>...</smiles> we provide uses SMILES (Simplified molecular-input line-entry system). To learn more about SMILES:

https://en.wikipedia.org/wiki/Simplified_molecular-input_line-entry_system

Note that SMILES is compatible with all major chemistry software.

You can additionally use the include_inchi parameter to include InChI data as XML attributes inside <smiles> elements, for examples <smiles inchi="..." inchikey="...">...</smiles>.

request

{
    "src": "https://mathpix.com/examples/chemistry_caffeine.png",
    "include_line_data": true,
    "include_smiles": true,
    "include_inchi": true
}

request image

response

{
    "request_id": "dbf6fa62120fc703735c9bffd1f793c5",
    "is_printed": true,
    "is_handwritten": false,
    "auto_rotate_confidence": 0.00038579112517922454,
    "auto_rotate_degrees": 0,
    "confidence": 0.5630934028128729,
    "confidence_rate": 0.5630934028128729,
    "text": "<smiles inchi=\"InChI=1S/C8H10N4O2/c1-10-4-9-6-5(10)7(13)12(3)8(14)11(6)2/h4H,1-3H3\" inchi_key=\"RYYVLZVUVIJVGH-UHFFFAOYSA-N\">Cn1c(=O)c2c(ncn2C)n(C)c1=O</smiles>",
    "line_data": [
        {
            "type": "diagram",
            "cnt": [
                [
                    436,
                    308
                ],
                [
                    32,
                    308
                ],
                [
                    32,
                    0
                ],
                [
                    436,
                    0
                ]
            ],
            "included": true,
            "subtype": "chemistry",
            "text": "\n<smiles>Cn1c(=O)c2c(ncn2C)n(C)c1=O</smiles>",
            "after_hyphen": false,
            "confidence": 0.5630934028128729,
            "confidence_rate": 0.9796978580652379
        }
    ]
}

rendered(response)

InChIKey

RYYVLZVUVIJVGH-UHFFFAOYSA-N

InChIKey values are convenient for searching online chemical databases, for example see:

https://webbook.nist.gov/cgi/cbook.cgi?InChI=RYYVLZVUVIJVGH-UHFFFAOYSA-N&Units=SI

limitations

does not support chemical reactions
struggles with huge molecules

Triangle diagrams

Geometry diagrams are treated just like other diagrams, except they also include a text field subtype in line_data which is equal to triangle (see here for docs). Like chemistry, they do not generate OCR results at the present time.

request

{
    "src": "https://mathpix.com/examples/triangle_0.jpg",
    "include_line_data": true
}

request image

response

{
    "is_printed": true,
    "is_handwritten": false,
    "auto_rotate_confidence": 0.007725002452811935,
    "auto_rotate_degrees": 0,
    "error": "Content not found",
    "error_info": {
        "id": "image_no_content",
        "message": "Content not found"
    },
    "line_data": [
        {
            "type": "diagram",
            "cnt": [
                [
                    339,
                    343
                ],
                [
                    31,
                    343
                ],
                [
                    31,
                    1
                ],
                [
                    339,
                    1
                ]
            ],
            "included": false,
            "subtype": "triangle",
            "error_id": "image_not_supported"
        }
    ]
}

Triangle diagram OCR

To enable triangle diagram OCR, include the include_geometry_data parameter in the main body of the request.

request

{
    "src": "https://mathpix.com/examples/triangle_0.jpg",
    "include_geometry_data": true
}

request image

response

{
    "is_printed": true,
    "is_handwritten": false,
    "auto_rotate_confidence": 0.03240217728347261,
    "auto_rotate_degrees": 0,
    "geometry_data": [
        {
            "position": {
                "top_left_x": 183,
                "top_left_y": 3,
                "height": 344,
                "width": 309
            },
            "shape_list": [
                {
                    "type": "triangle",
                    "vertex_list": [
                        {
                            "x": 218,
                            "y": 46,
                            "edge_list": [
                                1,
                                2
                            ]
                        },
                        {
                            "x": 218,
                            "y": 314,
                            "edge_list": [
                                0,
                                2
                            ]
                        },
                        {
                            "x": 456,
                            "y": 314,
                            "edge_list": [
                                0,
                                1
                            ]
                        }
                    ]
                }
            ],
            "label_list": [
                {
                    "position": {
                        "top_left_x": 198,
                        "top_left_y": 7,
                        "height": 24,
                        "width": 22
                    },
                    "text": "\\( A \\)",
                    "latex": "A",
                    "confidence": 0.99951171875,
                    "confidence_rate": 0.99951171875
                },
                {
                    "position": {
                        "top_left_x": 228,
                        "top_left_y": 78,
                        "height": 20,
                        "width": 14
                    },
                    "text": "\\( ? \\)",
                    "latex": "?",
                    "confidence": 0.96923828125,
                    "confidence_rate": 0.96923828125
                },
                {
                    "position": {
                        "top_left_x": 349,
                        "top_left_y": 154,
                        "height": 21,
                        "width": 16
                    },
                    "text": "6",
                    "latex": "6",
                    "confidence": 0.99951171875,
                    "confidence_rate": 0.99951171875
                },
                {
                    "position": {
                        "top_left_x": 189,
                        "top_left_y": 318,
                        "height": 24,
                        "width": 23
                    },
                    "text": "\\( C \\)",
                    "latex": "C",
                    "confidence": 0.837890625,
                    "confidence_rate": 0.837890625
                },
                {
                    "position": {
                        "top_left_x": 329,
                        "top_left_y": 326,
                        "height": 20,
                        "width": 18
                    },
                    "text": "4",
                    "latex": "4",
                    "confidence": 1,
                    "confidence_rate": 1
                },
                {
                    "position": {
                        "top_left_x": 469,
                        "top_left_y": 311,
                        "height": 22,
                        "width": 22
                    },
                    "text": "\\( B \\)",
                    "latex": "B",
                    "confidence": 0.99072265625,
                    "confidence_rate": 0.99072265625
                }
            ]
        }
    ]
}

rendered(response.geometry_data)

Visualization of the label and vertex predictions:

Line data

request

{
    "src": "https://mathpix.com/examples/text_with_math_1.jpg",
    "formats": ["html"],
    "include_line_data": true,
    "data_options": {
        "include_asciimath": true,
        "include_latex": true
    }
}

request image

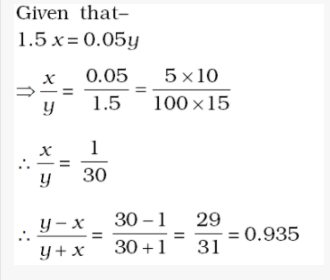
rendered(response.line_data[:].cnt)

This image the contours returned in the line_data field:

response

{
    "confidence": 0.9398651123046875,
    "confidence_rate": 0.9866095640316896,
    "html": "<div>Given that-<br>\n<span class=\"math-inline \">\n<asciimath style=\"display: none;\">1.5 x=0.05 y</asciimath><latex style=\"display: none\">1.5 x=0.05 y</latex></span><br>\n<span class=\"math-inline \">\n<asciimath style=\"display: none;\">=&gt;(x)/(y)=(0.05)/(1.5)=(5xx10)/(100 xx15)</asciimath><latex style=\"display: none\">\\Rightarrow \\frac{x}{y}=\\frac{0.05}{1.5}=\\frac{5 \\times 10}{100 \\times 15}</latex></span><br>\n<span class=\"math-inline \">\n<asciimath style=\"display: none;\">:.(x)/(y)=(1)/(30)</asciimath><latex style=\"display: none\">\\therefore \\frac{x}{y}=\\frac{1}{30}</latex></span><br>\n<span class=\"math-inline \">\n<asciimath style=\"display: none;\">:.(y-x)/(y+x)=(30-1)/(30+1)=(29)/(31)=0.935</asciimath><latex style=\"display: none\">\\therefore \\frac{y-x}{y+x}=\\frac{30-1}{30+1}=\\frac{29}{31}=0.935</latex></span></div>\n",
    "line_data": [
        {
            "type": "text",
            "cnt": [
                [
                    129,
                    20
                ],
                [
                    69,
                    21
                ],
                [
                    14,
                    21
                ],
                [
                    14,
                    3
                ],
                [
                    79,
                    2
                ],
                [
                    129,
                    2
                ]
            ],
            "included": true,
            "text": "Given that-",
            "after_hyphen": false,
            "confidence": 0.9398651123046875,
            "confidence_rate": 0.996560433820066,
            "html": "<div>Given that-</div>\n"
        },
        {
            "type": "math",
            "cnt": [
                [
                    139,
                    50
                ],
                [
                    16,
                    50
                ],
                [
                    16,
                    29
                ],
                [
                    139,
                    29
                ]
            ],
            "included": true,
            "text": "\n\\( 1.5 x=0.05 y \\)",
            "after_hyphen": false,
            "confidence": 1,
            "confidence_rate": 1,
            "html": "<div><span class=\"math-inline \">\n<asciimath style=\"display: none;\">1.5 x=0.05 y</asciimath><latex style=\"display: none\">1.5 x=0.05 y</latex></span></div>\n"
        },
        {
            "type": "math",
            "cnt": [
                [
                    231,
                    118
                ],
                [
                    13,
                    118
                ],
                [
                    13,
                    64
                ],
                [
                    231,
                    64
                ]
            ],
            "included": true,
            "text": "\n\\( \\Rightarrow \\frac{x}{y}=\\frac{0.05}{1.5}=\\frac{5 \\times 10}{100 \\times 15} \\)",
            "after_hyphen": false,
            "confidence": 1,
            "confidence_rate": 1,
            "html": "<div><span class=\"math-inline \">\n<asciimath style=\"display: none;\">=&gt;(x)/(y)=(0.05)/(1.5)=(5xx10)/(100 xx15)</asciimath><latex style=\"display: none\">\\Rightarrow \\frac{x}{y}=\\frac{0.05}{1.5}=\\frac{5 \\times 10}{100 \\times 15}</latex></span></div>\n"
        },
        {
            "type": "math",
            "cnt": [
                [
                    109,
                    190
                ],
                [
                    15,
                    190
                ],
                [
                    15,
                    138
                ],
                [
                    109,
                    138
                ]
            ],
            "included": true,
            "text": "\n\\( \\therefore \\frac{x}{y}=\\frac{1}{30} \\)",
            "after_hyphen": false,
            "confidence": 1,
            "confidence_rate": 1,
            "html": "<div><span class=\"math-inline \">\n<asciimath style=\"display: none;\">:.(x)/(y)=(1)/(30)</asciimath><latex style=\"display: none\">\\therefore \\frac{x}{y}=\\frac{1}{30}</latex></span></div>\n"
        },
        {
            "type": "math",
            "cnt": [
                [
                    300,
                    263
                ],
                [
                    15,
                    263
                ],
                [
                    15,
                    208
                ],
                [
                    300,
                    208
                ]
            ],
            "included": true,
            "text": "\n\\( \\therefore \\frac{y-x}{y+x}=\\frac{30-1}{30+1}=\\frac{29}{31}=0.935 \\)",
            "after_hyphen": false,
            "confidence": 0.99462890625,
            "confidence_rate": 0.9998776081738409,
            "html": "<div><span class=\"math-inline \">\n<asciimath style=\"display: none;\">:.(y-x)/(y+x)=(30-1)/(30+1)=(29)/(31)=0.935</asciimath><latex style=\"display: none\">\\therefore \\frac{y-x}{y+x}=\\frac{30-1}{30+1}=\\frac{29}{31}=0.935</latex></span></div>\n"
        }
    ]
}

rendered(response.text)

Given that-

1.5 x = 0.05 y

\Rightarrow \frac{x}{y} = \frac{0.05}{1.5} = \frac{5 \times 10}{100 \times 15}

∴ \frac{x}{y} = \frac{1}{30}

∴ \frac{y - x}{y + x} = \frac{30 - 1}{30 + 1} = \frac{29}{31} = 0.935